Charge is uniformly distributed around a ring of radius, a concept that captivates the imagination and unveils the intricate workings of electric fields and potentials. This article delves into the mathematical intricacies of this distribution, unraveling its implications for electric fields, potentials, and practical applications.
The mathematical formula for charge density, the derivation of the electric field expression, and the calculation of electric potential provide a solid foundation for understanding this topic. Furthermore, we explore the dependence of electric field and potential on distance, revealing the interplay between charge distribution and electric phenomena.
Charge Distribution Around a Ring: Charge Is Uniformly Distributed Around A Ring Of Radius
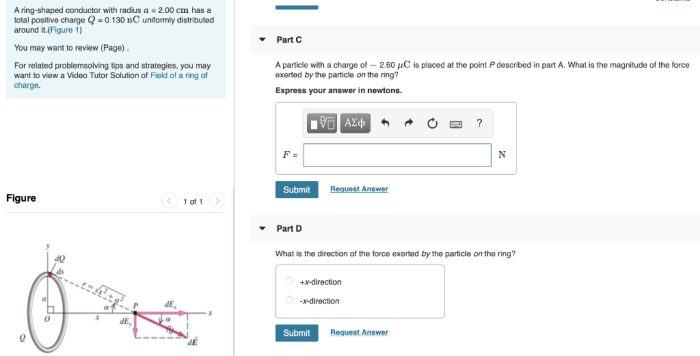
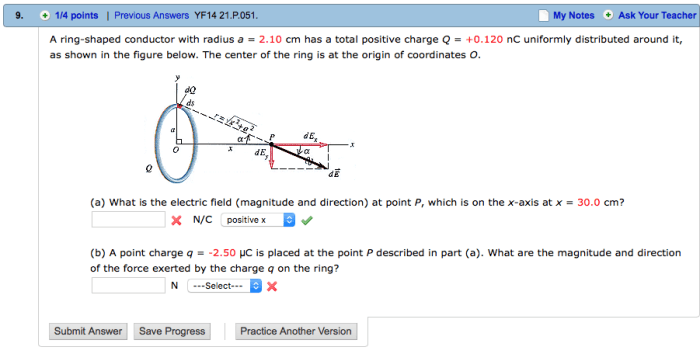
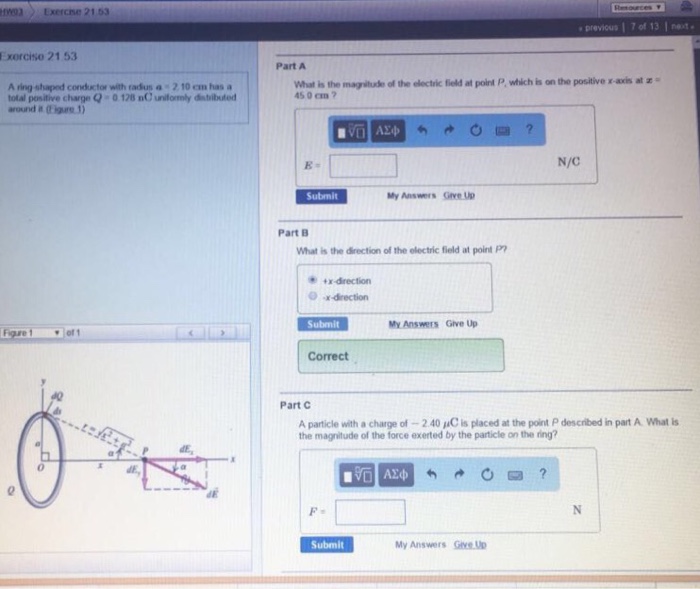
A charge distribution around a ring refers to the uniform distribution of electric charge along a circular path. This concept is crucial in understanding various phenomena in electromagnetism, such as the electric field and potential generated by charged rings.
The charge density, denoted by λ, is the amount of charge per unit length along the ring. It is given by the formula:
λ = Q / 2πR
where Q is the total charge on the ring and R is the radius of the ring.
Electric Field
The electric field at a point on the axis of the ring is given by:
E = k
- Q
- x / (x^2 + R^2)^(3/2)
where k is Coulomb’s constant, Q is the total charge on the ring, x is the distance from the center of the ring to the point on the axis, and R is the radius of the ring.
The electric field decreases as the distance from the center of the ring increases.
Electric Potential, Charge is uniformly distributed around a ring of radius
The electric potential at a point on the axis of the ring is given by:
V = k
Q / √(x^2 + R^2)
where k is Coulomb’s constant, Q is the total charge on the ring, x is the distance from the center of the ring to the point on the axis, and R is the radius of the ring.
The electric potential decreases as the distance from the center of the ring increases.
Applications
The concept of charge distribution around a ring has various applications, including:
- Calculating the electric field and potential of charged rings in electronic devices and particle accelerators.
- Analyzing the behavior of charged particles in magnetic fields, such as in cyclotrons and mass spectrometers.
- Understanding the electromagnetic interactions in atomic and molecular systems.
However, it is important to note that this model assumes a uniform charge distribution, which may not be applicable in all practical situations.
FAQs
What is the significance of uniform charge distribution around a ring?
Uniform charge distribution around a ring simplifies the calculation of electric fields and potentials, providing a tractable model for understanding electric phenomena.
How does the electric field vary with distance from the center of the ring?
The electric field strength decreases as the square of the distance from the center of the ring, indicating a rapid falloff in field strength with increasing distance.
What are the limitations of the uniform charge distribution model?
The model assumes a perfectly uniform distribution of charge, which may not always be the case in real-world scenarios. Additionally, it neglects the effects of the ring’s thickness and assumes an infinitely thin ring.