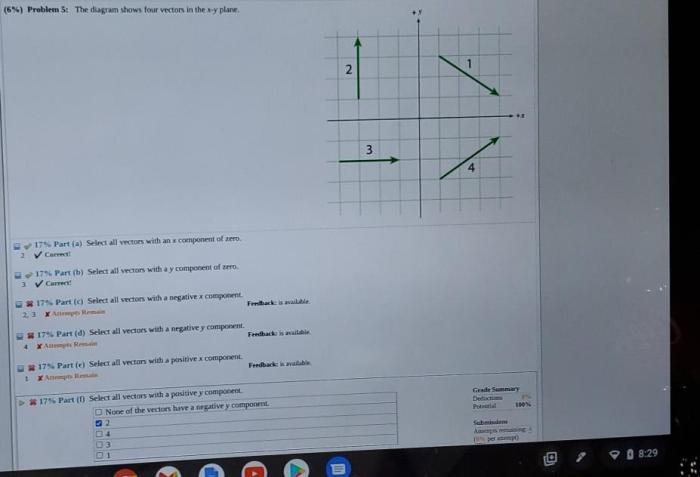
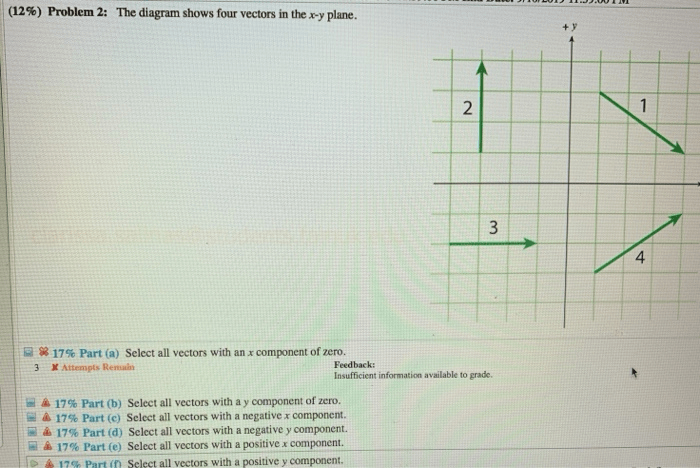
Select all vectors with an x component of zero – Embark on a journey into the realm of linear algebra and vector mathematics, where we delve into the intricacies of selecting vectors with a zero x component. This concept finds widespread applications in diverse fields, from physics and engineering to computer graphics.
Join us as we unravel the mathematical foundations, explore real-world applications, and uncover the geometric interpretations associated with this fundamental concept.
At the heart of this exploration lies the notion of the ‘x component’ of a vector, which represents its projection onto the x-axis in a coordinate system. Understanding the x component is crucial for comprehending the behavior and relationships of vectors in various contexts.
Define and Explain ‘x component’
In linear algebra and vector mathematics, the x component of a vector is the projection of the vector onto the x-axis of a coordinate system. It represents the horizontal component of the vector’s displacement or magnitude.
For a vector v = (x, y, z), the x component is simply the first coordinate, denoted as v x= x.
Examples, Select all vectors with an x component of zero
- A vector with a non-zero x component: v = (3, 4, 5) has v x= 3.
- A vector with a zero x component: v = (0, 5, 2) has v x= 0.
Identify Vectors with Zero X Component

Mathematical Formula
A vector v = (x, y, z) has a zero x component if and only if v x= x = 0.
Selection Algorithm
- For each vector v = (x, y, z) in a given set of vectors:
- If vx= x = 0, then select v as a vector with a zero x component.
Applications and Examples: Select All Vectors With An X Component Of Zero
Selecting vectors with a zero x component is useful in various applications:
- Physics:Identifying particles or objects moving only in the y-z plane.
- Engineering:Analyzing forces acting in specific directions.
- Computer Graphics:Creating 2D projections of 3D objects.
Visualization and Geometric Interpretation
In a 2D coordinate system, vectors with a zero x component are parallel to the y-axis. They form a vertical line passing through the origin.
In a 3D coordinate system, vectors with a zero x component lie in the yz-plane. They form a plane parallel to the x-axis.
Vector Operations and Implications
- Addition:Adding two vectors with zero x components results in a vector with a zero x component.
- Subtraction:Subtracting two vectors with zero x components results in a vector with a zero x component.
- Scalar Multiplication:Multiplying a vector with a zero x component by a scalar results in a vector with a zero x component.
Extensions and Generalizations
The concept of a zero x component can be extended to higher dimensions and more complex vector spaces.
For example, in a 4D vector space, vectors with a zero x component would lie in the 3D subspace defined by the y, z, and w axes.
Top FAQs
What is the significance of selecting vectors with a zero x component?
Selecting vectors with a zero x component allows for the isolation and analysis of vectors that lie parallel to the y-z plane in a coordinate system. This is particularly useful in applications where the x-axis is not relevant or can be ignored.
How is the x component of a vector determined?
The x component of a vector is the projection of the vector onto the x-axis. It can be calculated using the dot product between the vector and the unit vector along the x-axis.
What are some practical applications of selecting vectors with a zero x component?
Selecting vectors with a zero x component finds applications in various fields, including physics, engineering, and computer graphics. For instance, in physics, it can be used to analyze the motion of objects in two dimensions, while in engineering, it can be employed to design structures that are stable in the presence of lateral forces.